Tugas Matematika: MATRIK, MACAM-MACAM MATRIK DAN OPERASI MATRIK

MATRIK, MACAM-MACAM MATRIK DAN OPERASI MATRIK

Nama : Muhamad Rayyen Alfareza Bukhari

Kelas : XI IPS 2

Absen : 21

A. Pengertian Matriks

Matriks adalah sebuah susunan bilangan-bilangan dalam baris dan kolom yang berbentuk persegi panjang.

Baris pada sebuah matriks adalah susunan bilangan-bilangan yang mendatar dalam matriks. Sedangkan Kolom pada sebuah matriks adalah susunan bilangan-bilangan yang tegak dalam matriks.

Susunan bilangan dalam matriks ini diletakkan didalam kurung biasa “( )” atau kurung siku “[ ]”.

Dalam penamaan suatu matriks biasanya dinyatakan dengan huruf kapital, misalnya matriks A,

B, C, D, ..., dan seterusnya.

Dalam matriks dikenal dengan istilah ordo. Ordo matriks adalah bilangan yang menunjukkan banyaknya baris (m) dan banyaknya kolom (n) pada matriks.

contoh : Suatu matrik A dengan m baris dan n kolom ditulis

Misalnya diberikan sebuah matriks A sebagai berikut

Matriks A diatas terdiri dari 4 baris dan 3 kolom, sehingga disebut matriks berordo 4x3 dan dapat ditulis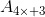

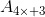
B. Jenis-jenis Matriks

Matriks memilik banyak jenis yang dapat dibedakan dengan ordo dan elemen-elemennya. Jenis matriks adalah sebagai berikut.

1. Matriks baris.

Matriks yang terdiri dari satu baris. Contoh :

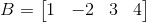
2. Matriks kolom.

Matriks yang terdiri dari satu kolom. Contoh :

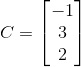
3. Matriks persegi.

Matriks yang banyak baris sama dengan banyak kolom. Contoh :

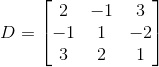
4. Matriks nol.

Matriks yang semua elemennya nol. Contoh :

5. Matriks identitas.

Matriks yang elemen diagonal utamanya sama dengan 1, sedangkan elemen-elemen lainnya sama dengan 0. Contoh :

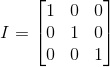
6. Matriks Skalar.

Matriks yang elemen diagonal utamanya sama, sedangkan elemen di luar elemen diagonalnya bernilai nol. Contoh :

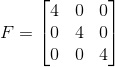
7. Matriks diagonal.

Matriks persegi memiliki elemen di luar diagonal utama yang bernilai nol. Contoh :

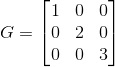
8. Matriks segitiga atas.

Matriks persegi yang elemen diagonal bawah bernilai nol. Contoh :

9. Matriks segitiga bawah.

Matriks persegi yang elemen diagonal atas bernilai nol. Contoh :

10. Transpos matriks A atau (A t).

Matriks yang disusun dengan cara menuliskan baris ke-i matriks A menjadi kolom ke-i dan sebaliknya, menuliskan kolom ke-j matriks A menjadi baris ke-j

Misalnya, jika matriks A

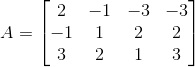
maka matriks transpos dari A adalah :

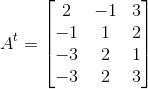
C. Operasi pada Matriks

1. Penjumlahan Matriks

Syarat pada penjumlahan matriks ialah harus memiliki ordo yang sama, dan menambahkan pada posisi atau letak yang sama. Contohnya sebagai berikut :

2. Pengurangan Matriks

Syarat pada pengurangan matriks juga sama dengan penjumlahan. Misal matriks C adalah pengurangan matriks A dan B, perlu kita ketahui bahwa matriks pengurangan ialah sama dengan penambahan Matriks A dengan perkalian skalar -1 dengan matriks B.

"C=A-B" sama dengan "C = A+ [-1] B"

Contoh pengurangan matriks sebagai berikut :

3. Perkalian matriks dengan skalar

Pada perkalian matriks dengan skalar caranya yaitu mengalikan nilai skalar dengan semua letak matriks. Contohnya sebagai berikut :

4. Perkalian matriks dengan matriks

Syarat pada perkalian matriks ialah jumlah kolom pada matriks pertama sama dengan jumlah baris pada matriks kedua. Contohnya sebagai berikut perkalian A2x3 dan 3x3 :

D. Contoh Soal

1. Jika diketahui persamaan metrik !

Pembahasannya :

Karena kedua matriks sama, maka elemen-elemen yang seletak akan sama pula, sehingga berlaku:

2x + 1 = 3
2x = 2
x = 1
y + 12 = 15
y = 3
x + y = 1 + 3 = 4

2. Jika determinan nilai matriks A adalah 4 kali determinan nilai matriks B, maka nilai x adalah…

Pembahasannya:
det A = 4 det B
4 x (16 x ) – (-16) = 4 (108 – (-152))
4 x (4 2x ) + 16 = 4 (260)
4 3x = 4 (260) – 16
4 3x = 4 (260) – 4 (4)
4 3x = 4 (260 – 4)
4 3x = 4 (256)
4 3x = 4. 4 4
4 3x = 4 5
3x = 5
x = 5/3

3. Jika matriks $\begin{pmatrix} 9 & 7 \\ 5 & 4 \end{pmatrix}$ dan $\begin{pmatrix} x-1 & x-12 \\ -x & x+4 \end{pmatrix}$ saling invers, tentukan nilai x!