Assalamualaikum wr.wb

Nama : Muhamad Rayyen Alfareza Bukhari (22)

Kelas : XI IPS 2 

MENGGAMBAR GRAFIK FUNGSI DENGAN TURUNAN PERTAMA DAN TURUNAN KEDUA

Langkah-langkah menggambar grafik fungsi menggunakan turunan :

1. Menentukan titik potong dengan sumbu-sumbu koordinat (sumbu x dan sumbu y)

    Titik potong sumbu x, subsitusi y = 0

    Titik potong sumbu y, subsitusi x = 0

2. Menentukan titik-titik stasioner dan jenisnya (titik balik minimun, titik balik maksimum 

    dan titik belok)

3. Menentukan titik bantuan lainnya agar membuat grafiknya lebih mudah atau bisa juga

   secara umum menentukan nilai y untuk  besar x positif dan  besar x negatif.

Contoh soal :

1). Gambarlah grafik kurva y=3x2−x3

 Penyelesaian : i). Menentukan titik potong pada sumbu-sumbu : *). Tipot sumbu X, substitusi y=0

y=0 y=0→y 0=3x2−x3

3x2−x3=0

x2(3−x)

x=0 ∨ x =3

 Sehingga titik potong sumbu X adalah (0,0) dan (3,0).

*). Tipot sumbu Y, substitusi x=0

 y=3x2−x3 = 3.02−03 = 0y = 3x2−x3 = 3.02−03 = 0

 Sehingga titik potong sumbu Y adalah (0,0).

 ii). Menentukan titik-titik stasioner,

 Fungsi : y=3x2−x3 f′(x)=6x−3x2f′(x)=6x−3x2 dan f′′(x)=6−6x

 *). Syarat stasioner : f′(x)=0

f′(x)=0 6x−3x2=0

3x(2−x)=0

x=0 v x =2

Untuk x=0x=0 , nilai stasionernya f(0)=3.02−03=0 titik stasionernya (0,0) . Untuk x=2x=2 , nilai stasionernya f(2)=3.22−23=4 titik stasionernya (2,4).

 *). Menentukan jenis stasionernya, gunakan turunan kedua : f′′(x)=6−6xf′′(x)=6−6x Untuk x=0→f′′(0)=6−6.0=6x=0→f′′(0)=6−6.0=6 (positif) , jenisnya minimum. Untuk x=2→f′′(2)=6−6.2=−6x=2→f′′(2)=6−6.2=−6 (negatif) , jenisnya maksimum. Artinya titik (0,0) adalah titik balik minimum dan titik (2,4) adalah titik balik maksimum.

 iii). Berdasarkan fungsi y=3x2−x3,y=3x2−x3, kita substitusi beberapa nilai xx yaitu : Untuk xx semakin besar, nilai yy semakin besar negatif (ke bawah) dan untuk xxsemakin kecil, nilai yy semakin besar positif (ke atas).

2. Gambarkan grafik berikut dengan menggunakan konsep turunan.
Titik stasioner diperoleh berada di titik (1, -1) sebagai berikut:
Interval naik atau turun pada fungsi:
Pada fungsi tidak terdapat titik belok karena 2 tidak sama dengan nol, sepertii berikut:Titik optimum berada di titik (1, -1) dengan melakukan uji titik stasioner ke turunan kedua fungsi, , dimana f''(x)=2>0. Sehingga grafik fungsi dengan konsep turunan pada soal dapat kita gambarkan seperti di bawah ini:

Soal Pilhan Ganda :

1. Grafik dibawah adalah grafik fungsi $\cdots \cdot$

A. $y=2\sin x,0^{\circ }\le x\le {270}^{\circ }$
B. $y=2\cos 4x,0^{\circ }\le x\le {270}^{\circ }$
C. $y=4\sin 2x,0^{\circ }\le x\le {270}^{\circ }$
D. $y=4\cos 2x,0^{\circ }\le x\le {270}^{\circ }$
E. $y=4\sin 4x,0^{\circ }\le x\le {270}^{}$

Pembahasan

Perhatikan sketsa gambar berikut.

Beranjak dari grafik sinus yang memiliki bentuk umum $f\left(x\right)=a\sin kx$, kurva pada gambar tidak bergeser dan berawal dari titik $(0,0)$. Grafik juga menunjukkan bahwa nilai maksimum dan minimum fungsi adalah $4$ dan $-4$, sehingga

$\begin{array}{cc}a& =\frac{\text{N. Maksimum}-\text{N. Minimum}}{2}\\ & =\frac{4-(-4)}{2}=4\end{array}$
Pada saat nilai $x={180}^{\circ }$, fungsi kembali bernilai $0$, lalu berulang kembali seperti sebelumnya, sehingga periodenya adalah ${180}^{\circ }$, dan akibatnya
$k=\frac{{360}^{\circ }}{{180}^{\circ }}=2$
Jadi, rumus fungsi $f\left(x\right)=4\sin 2x$ dengan batas interval $0^{\circ }\le x\le {270}^{\circ }$
(Jawaban C)

 2. Diketahui $f\left(x\right)=\cos x+3$ dengan $0\le x\le 2\pi$. Daerah hasil fungsi $f\left(x\right)$ adalah $\cdots \cdot$
A. $-3\le f\left(x\right)\le 3$              D. $0\le f\left(x\right)\le 3$
B. $-2\le f\left(x\right)\le 2$              E. $2\le f\left(x\right)\le 4$
C. $-1\le f\left(x\right)\le \; 1$

Pembahasan

Agar $f\left(x\right)=\cos x+3$mencapai maksimum, maka $\cos x$ haruslah sebesar-besarnya, yaitu $\cos x=1$. Untuk itu,

$f_{\text{maks}}\left(x\right)=1+3=4$
Agar $f\left(x\right)=\cos x+3$ mencapai minimum, maka $\cos x$ haruslah sekecil-kecilnya, yaitu $\cos x=-1$. Untuk itu,
$f_{\text{min}}\left(x\right)=-1+3=2$
Jadi, daerah hasil fungsi $f\left(x\right)$ adalah semua nilai (bilangan real) dari $2$ sampai $4$, atau secara matematis ditulis $2\le f\left(x\right)\le 4$
(Jawaban E)

3. Perhatikan grafik berikut.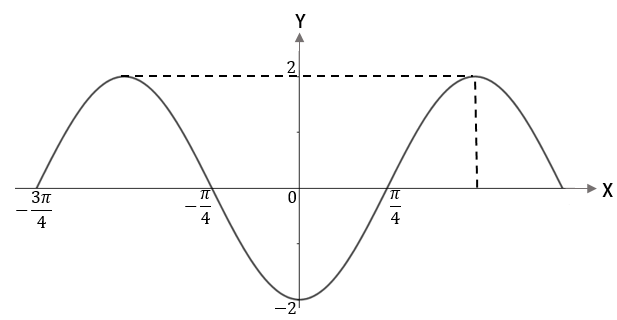

Fungsi yang memenuhi grafik di atas adalah $\cdots \cdot$
A. $f\left(x\right)=-2\sin (x-\frac{\pi }{4})$
B. $f\left(x\right)=-2\sin (x+\frac{\pi }{4})$
C. $f\left(x\right)=-2\sin (2x-\frac{\pi }{2})$
D. $f\left(x\right)=-2\sin (2x+\frac{\pi }{2})$
E. $f\left(x\right)=-2\sin (2x-\frac{\pi }{4}$)

Pembahasan

Beranjak dari grafik sinus: karena kurva bergeser (ke kiri) sejauh $\frac{\pi }{4}$, maka bentuk umum grafik fungsinya adalah $f\left(x\right)=y=a\sin k(x-c)$. 

Untuk grafik ini, nilai $c$ yang menentukan pergeseran kurva adalah $-\frac{\pi }{4}$. Dimulai dari titik $x=-\frac{3\pi }{4}$yang nilai fungsinya 0, grafik fungsi kembali bernilai $0$ dan berulang kembali di titik $x=\frac{\pi }{4}$, sehingga periode grafik fungsinya adalah $\frac{\pi }{4}–(-\frac{3\pi }{4})=\pi$.

Dengan demikian,
$k=\frac{2\pi }{\text{Periode}}=\frac{2\pi }{\pi }=2$
Nilai $a$ ditentukan oleh nilai maksimum dan nilai minimum fungsi, yakni
$\begin{array}{cc}a& =\frac{\text{N. Maksimum}-\text{N. Minimum}}{2}\\ & =\frac{2-(-2)}{2}=2\end{array}$
Catatan: Pilihan ganda pada soal menunjukkan bahwa $a=-2$, artinya kurva sinus menurun, lalu menanjak. Ini menjadi alasan mengapa kita anggap kurva bergeser ke kiri.
Jadi, rumus grafik fungsinya adalah$$f\left(x\right)=-2\sin 2(x+\frac{\pi }{4})=-2\sin (2x+\frac{\pi }{2})$$(Jawaban D)

  

 

Sekian Blog untuk materi hari ini kurang lebihnya mohon maaf 

Jangan lupa tersenyum :) dan selalu semangat

Wassalamualaikum wr.wb 

DAFTAR PUSTAKA : 

https://mathcyber1997.com/soal-dan-pembahasan-fungsi-trigonometri-dan-grafiknya/   

https://www.kompas.com/skola/read/2020/11/18/174944769/menggambar-grafik-fungsi-pada-konsep-turunan?page=all 

https://novandhikarf.wixsite.com/home/post/grafik-turunan